軌跡とは何か
平面上で,与えられた条件を満たしながら点$P$が動くとき,点$P$の描く図形を, その条件を満たす点の軌跡 (locus)という.
2点から等距離にある点の軌跡
座標平面上の2点$A(-1,~4),B(3,~2)$から等距離にある点$P$の軌跡を求めよ.
無題
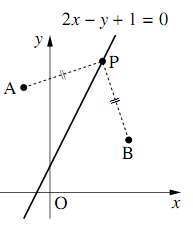
点$P$の座標を$(x,~y)$とすると,
$AP = BP$より,$AP^2 = BP^2$だから
\begin{align} &(x+1)^2+(y-4)^2\\ &=(x-3)^2+(y-2)^2\\ \Leftrightarrow~&2x-y+1=0 \end{align}より,求める軌跡は,直線$\boldsymbol{2x-y+1=0}$である.
アポロニウスの円〜その1〜
座標平面上2点$A(1,~3),B(4,-3)$からの距離の比が$1:2$である点$P$の軌跡を求めよ.
無題
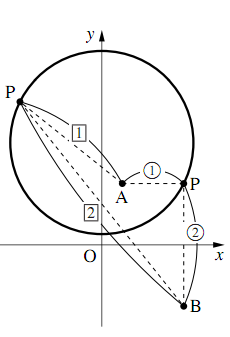
$AP:BP = 1:2$つまり,$2AP = BP$だから,
$4AP^2 = BP^2$
$P(x,~y)$とすると
$\text{AP}^2=(x-1)^2 +(y-3)^2$ $\tag{1}\label{aporoniusunoensono1nokaitou1}$
←座標平面上の2点間の距離
$\text{BP}^2=(x-4)^2 +(y+3)^2$ $\tag{2}\label{aporoniusunoensono1nokaitou2}$
であるから
\begin{align} &4\left\{(x-1)^2 +(y-3)^2\right\} \\ &=(x-4)^2 +(y+3)^2\\ \Leftrightarrow~&4(x^2-2x+1) + 4(y^2 -6y+9)\\ &=x^2 -8x+16+y^2 +6y+9\\ \Leftrightarrow~&3x^2 +3y^2 -30y+40-25=0\\ \Leftrightarrow~&x^2 +y^2 -10y +5=0\\ \Leftrightarrow~&x^2 +(y-5)^2=20 \end{align}よって,求める軌跡は,
中心$(0,~5)$半径$2\sqrt{5}$の円
である.
2点からの距離の比が与えられたときの点の軌跡について,一般に次のことが成り立つ.
アポロニウスの円
2点$A,B$からの距離の比が$m:n$である点$P$の軌跡は,$m\neq n$のとき, 線分$AB$を$m:n$に内分する点と外分する点を直径の両端とする円である. この円をアポロニウスの円 (circle of Apollonius)という.
なお,$m=n$のときは,2つ上の例題でみたように,線分$AB$の垂直二等分線となる.
アポロニウスの円〜その2〜
上のアポロニウスの円〜その1〜の例題を,アポロニウスの円の知識を使って解け.
無題
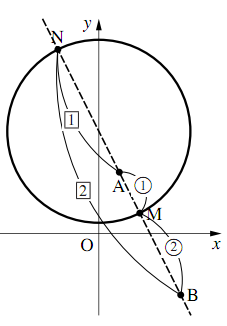
線分$AB$を$1:2$に内分する点$M$の座標は
\begin{align} &\left(\dfrac{1\times2+4\times1}{1+2},~\dfrac{3\times2-3\times1}{1+2}\right)\\ &=(2,~1) \end{align}外分する点$N$の座標は
\begin{align} &\left(\dfrac{1\times2+4\times(-1)}{-1+2},~\dfrac{3\times2-3\times(-1)}{-1+2}\right)\\ &=(-2,~9) \end{align}軌跡である円の直径となる$MN$の距離は
\begin{align} \sqrt{(2+2)^2+(1-9)^2}=\sqrt{80}=4\sqrt{5} \end{align}軌跡である円の中心となる$MN$の中点の座標は
\begin{align} \left(\dfrac{2-2}{2},~\dfrac{1+9}{2}\right)=(0,~5) \end{align}よって,求める軌跡は,
中心$(0,~5)$半径$2\sqrt{5}$の円
である.