軌跡
軌跡とは何か
平面上で,与えられた条件を満たしながら点$P$が動くとき,点$P$の描く図形を, その条件を満たす点の軌跡 (locus)という.
2点から等距離にある点の軌跡
座標平面上の2点$A(-1,~4),B(3,~2)$から等距離にある点$P$の軌跡を求めよ.
無題
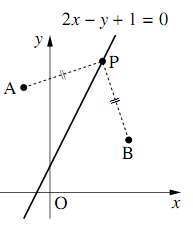
点$P$の座標を$(x,~y)$とすると,
$AP = BP$より,$AP^2 = BP^2$だから
\begin{align} &(x+1)^2+(y-4)^2\\ &=(x-3)^2+(y-2)^2\\ \Leftrightarrow~&2x-y+1=0 \end{align}より,求める軌跡は,直線$\boldsymbol{2x-y+1=0}$である.
アポロニウスの円〜その1〜
座標平面上2点$A(1,~3),B(4,-3)$からの距離の比が$1:2$である点$P$の軌跡を求めよ.
無題
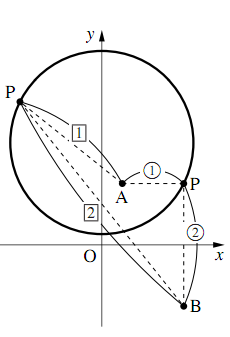
$AP:BP = 1:2$つまり,$2AP = BP$だから,
$4AP^2 = BP^2$
$P(x,~y)$とすると
$\text{AP}^2=(x-1)^2 +(y-3)^2$ $\tag{1}\label{aporoniusunoensono1nokaitou1}$
←座標平面上の2点間の距離
$\text{BP}^2=(x-4)^2 +(y+3)^2$ $\tag{2}\label{aporoniusunoensono1nokaitou2}$
であるから
\begin{align} &4\left\{(x-1)^2 +(y-3)^2\right\} \\ &=(x-4)^2 +(y+3)^2\\ \Leftrightarrow~&4(x^2-2x+1) + 4(y^2 -6y+9)\\ &=x^2 -8x+16+y^2 +6y+9\\ \Leftrightarrow~&3x^2 +3y^2 -30y+40-25=0\\ \Leftrightarrow~&x^2 +y^2 -10y +5=0\\ \Leftrightarrow~&x^2 +(y-5)^2=20 \end{align}よって,求める軌跡は,
中心$(0,~5)$半径$2\sqrt{5}$の円
である.
2点からの距離の比が与えられたときの点の軌跡について,一般に次のことが成り立つ.
アポロニウスの円
2点$A,B$からの距離の比が$m:n$である点$P$の軌跡は,$m\neq n$のとき, 線分$AB$を$m:n$に内分する点と外分する点を直径の両端とする円である. この円をアポロニウスの円 (circle of Apollonius)という.
なお,$m=n$のときは,2つ上の例題でみたように,線分$AB$の垂直二等分線となる.
アポロニウスの円〜その2〜
上のアポロニウスの円〜その1〜の例題を,アポロニウスの円の知識を使って解け.
無題
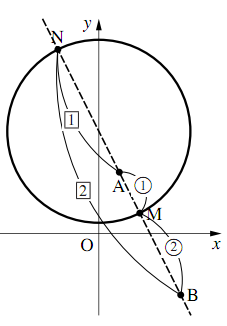
線分$AB$を$1:2$に内分する点$M$の座標は
\begin{align} &\left(\dfrac{1\times2+4\times1}{1+2},~\dfrac{3\times2-3\times1}{1+2}\right)\\ &=(2,~1) \end{align}外分する点$N$の座標は
\begin{align} &\left(\dfrac{1\times2+4\times(-1)}{-1+2},~\dfrac{3\times2-3\times(-1)}{-1+2}\right)\\ &=(-2,~9) \end{align}軌跡である円の直径となる$MN$の距離は
\begin{align} \sqrt{(2+2)^2+(1-9)^2}=\sqrt{80}=4\sqrt{5} \end{align}軌跡である円の中心となる$MN$の中点の座標は
\begin{align} \left(\dfrac{2-2}{2},~\dfrac{1+9}{2}\right)=(0,~5) \end{align}よって,求める軌跡は,
中心$(0,~5)$半径$2\sqrt{5}$の円
である.
条件に動点を含む場合の軌跡
次の例題の点$Q$のように,条件に動点を含む場合はその座標を$(X,~Y)$などとおき計算していく.
条件に動点を含む場合の軌跡
円$x^2+y^2=4$と点$A(4,~0)$がある. 点$Q$がこの円上を動くとき,線分$AQ$を$3:1$に内分する点$P$の軌跡を求めよ.
無題

点$P,Q$の座標をそれぞれ$(x,~y),(X,~Y)$とする.
点$Q$は円$x^2+y^2=4$上にあるから
\begin{align} X^2+Y^2=4 \end{align} $\tag{1}\label{joukennidoutenwohukumubaainokisekinokaitou1}$点$P$は線分$AQ$を$3:1$に内分する点だから
\begin{align} X&=\dfrac{1\times4+3X}{3+1}~,\\ y&=\dfrac{1\times0+3Y}{3+1} \end{align} $\tag{2}\label{joukennidoutenwohukumubaainokisekinokaitou2}$よって,$X=\dfrac{4}{3}x-\dfrac{4}{3},Y=\dfrac{4}{3}y$.これらを$\eqref{joukennidoutenwohukumubaainokisekinokaitou1}$に代入すると
←なぜこのような操作を行うのかについては下の本文を参照
\begin{align} &\left(\dfrac{4}{3}x-\dfrac{4}{3}\right)^2+\left(\dfrac{4}{3}y\right)^2=4\\ \Leftrightarrow~&(x-1)^2+y^2=\dfrac{9}{4} \end{align}よって,求める軌跡は,
中心が$(1,~0)$半径が$\dfrac{3}{2}$の円
である.
上の例題の軌跡,つまり点$P$の決まり方は,問題文をそのままに読めば,まず点$Q$が決まり次に点$P$が決まるという順序になっている. しかし,このような理解では,無数の点$Q$に対して点$P$をプロットすることしかできず,軌跡の一端は垣間見えるものの, 図形の方程式としては求まらない.
そこで,考え方の順序を変え,ある点$P(x,~y)$を考えてみてそれが軌跡上にあるかどうか調べるという方法をとる . たとえば,点$P(1,~2)$が軌跡上にあるかどうかを調べてみよう. $AP:AQ = 3:1$であるから,例題中の$\eqref{joukennidoutenwohukumubaainokisekinokaitou2}$に$(1,~1)$を代入して
\begin{align} 1=\dfrac{1\times4+3X}{3+1}~,~~2=\dfrac{1\times0+3Y}{3+1} \end{align}を満たさなくてはならない. この式から$X$と$Y$は,$(X,~Y)=\left(0,~\dfrac{8}{3}\right)$であることが必要となるが, これらをそもそも円$x^2 + y^2 = 4$上にあるので,例題中の$\eqref{joukennidoutenwohukumubaainokisekinokaitou1}$を満たさなければならないが, 代入しても
\begin{align} 0+\left(\dfrac{8}{3}\right)^2\neq 4 \end{align}となり満たさないので,点$(1,~2)$は軌跡に含まれない(満たせば軌跡に含まれる).
このような作業を具体的な点$(1,~1)$ではなく,ある点$(x,~y)$で行うことにより,$x$と$y$が満たす方程式が 得られ軌跡を求めることができる.
このような考え方を使う例題として,もう1問練習してみよう.
2直線の交点の軌跡
2直線$l_1:kx+y+1=0,l_2:x-ky-1=0$の交点$P$が描く軌跡を求めよ.
無題

方程式を
\begin{cases} kx+y+1=0\\ x-ky-1=0 \end{cases}上の式を$\tag{1}\label{2chokusennokoutennokisekinokaitou1}$,下の式を$\tag{2}\label{2chokusennokoutennokisekinokaitou2}$としておく.
1)$y\neq 0$のとき,$\eqref{2chokusennokoutennokisekinokaitou2}$より
\begin{align} k=\dfrac{x_1}{y}~~(y\neq 0) \end{align}これを$\eqref{2chokusennokoutennokisekinokaitou1}$に代入して
\begin{align} &\dfrac{x_1}{y}\cdot x +y+1 =0 \\ \Leftrightarrow~&x^2 -x +y^2 +y=0\\ \Leftrightarrow~&\left(x-\dfrac{1}{2} \right)^2 +\left( y+\dfrac{1}{2}\right)^2 =\dfrac{1}{2} \end{align}2)$y = 0$のとき,$\eqref{2chokusennokoutennokisekinokaitou2}$より$x = 1$が必要だが, これは,$\eqref{2chokusennokoutennokisekinokaitou1}$で$k = − 1$のとき成立する. つまり,点$(1,~0)$は$l_1$と$l_2$の交点である.
以上1),2)より,求める軌跡は,
中心$\left(\dfrac{1}{2},~-\dfrac{1}{2}\right)$半径$\dfrac{1}{\sqrt{2}}$の円
(ただし,点$(0,~0)$を除く)
となる.