$90^\circ+\theta$ の三角比
図のように、単位円周上に角$\theta$ の動径 $\text{OP}$ と角 $90^\circ+\theta(=\theta'とする)$ の動径 $\text{OP'}$ をとる。
$90^\circ+\theta$ の三角比
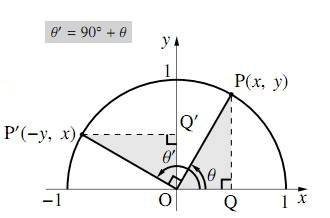
点 $\text{P}$ の座標を $(x,y)$ とすると、$\triangle\text{OPQ}$ と $\triangle\text{OP'Q'}$ は合同なので、点 $\text{P'}$ の座標は $(-y,x)$ となるから \[\sin\theta'=x=\cos\theta\] \[\cos\theta'=y=-\sin\theta\] \[\tan\theta'=\dfrac{x}{-y}=-\dfrac{x}{y}=-\dfrac{1}{\tan\theta}\] と表すことができる。
ここで、$\theta'=90^\circ+\theta$ であるから、次のようにまとめることができる。
$90^\circ+\theta$ の三角比
$90^\circ+\theta$ の三角比
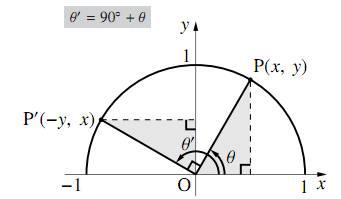
角 $\theta$ が $0^\circ\leqq\theta\leqq90^\circ$ の三角比において \[\sin(90^\circ+\theta)=\cos\theta\] \[\cos(90^\circ+\theta)=-\sin\theta\] \[\tan(90^\circ+\theta)=-\dfrac{1}{\tan\theta}\] が成り立つ。
吹き出し$90^\circ+\theta$ の三角比
「$90^\circ+\theta$ の三角比は $\theta$ だけを使った三角比で表せる」ということを覚えておくのが大切であり、この式は暗記するようなものではない。必要なときに、上の図を描いて素早く導出できるようにしておけばよい。
これより、$90^\circ\lt\theta\leqq180^\circ$ の三角比は、$0^\circ\lt\theta\leqq90^\circ$ の三角比になおして、その値を求めることができる。
$90^\circ+\theta$ の三角比の利用
次の式を満たすように $\fbox{A}$ の中に $90^\circ$ より小さい角を入れよ。
- $\sin100^\circ=\cos\fbox{A}$
- $\cos179^\circ=-\sin\fbox{A}$
- $\tan125^\circ=-\dfrac{1}{\tan\fbox{A}}$
- $\blacktriangleleft$ $\sin(90^\circ+\theta)=\cos\theta$$\sin100^\circ=\sin(90^\circ+10^\circ)=\cos10^\circ$
- $\blacktriangleleft$ $\cos(90^\circ+\theta)=-\sin\theta$$\cos179^\circ=\cos(90^\circ+89^\circ)=-\sin89^\circ$
- $\blacktriangleleft$ $\tan(90^\circ+\theta)=-\dfrac{1}{\tan\theta}$$\tan125^\circ=\tan(90^\circ+35^\circ)=-\dfrac{1}{\tan35^\circ}$