円と三角形

円周角の定理

円周角の定理

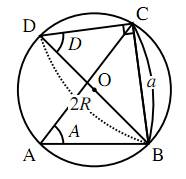
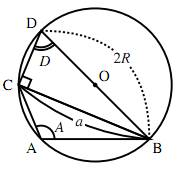
円周角の定理

無題

無題

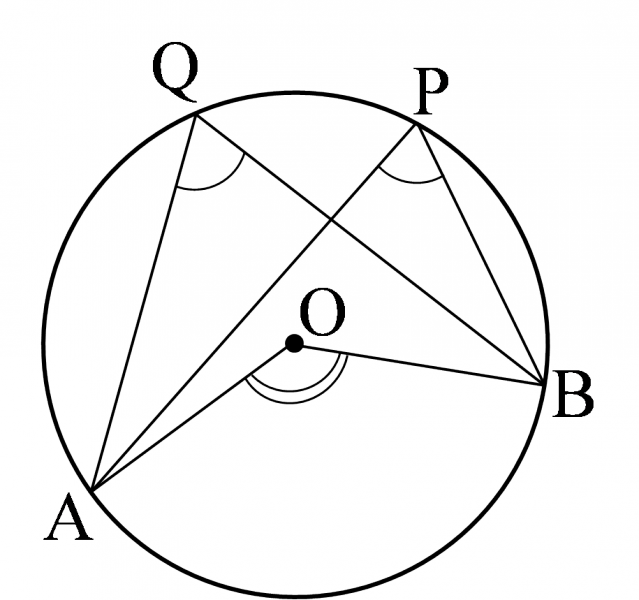
1つの弧に対する円周角の大きさは一定であり，その弧に対する中心角の大きさの半分である．

円周角の定理

次の図で， $\angle{x}$ の大きさを求めよ．

  1. $48^\circ$
  2. $132^\circ$
  3. $105^\circ$
  4. $112^\circ$
  5. $70^\circ$
  6. $50^\circ$

円周角の定理の逆

無題

無題

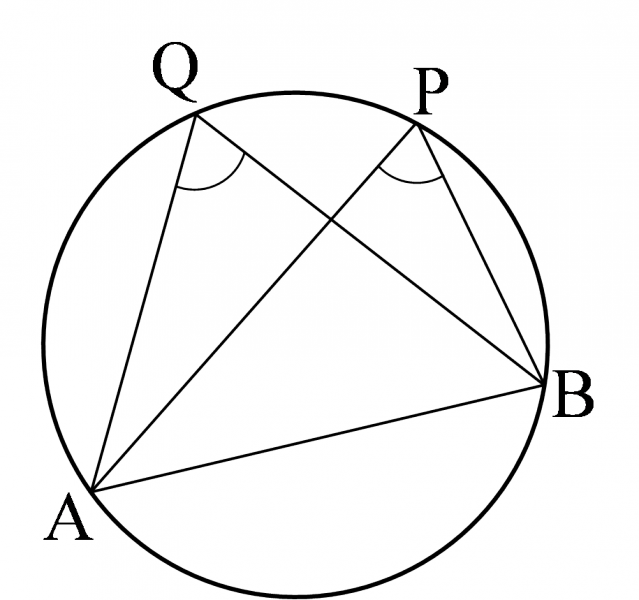
4点 $\mathrm{A},\mathrm{B},\mathrm{P},\mathrm{Q}$ について，点 $\mathrm{P},\mathrm{Q}$ が直線 $\mathrm{AB}$ に関して同じ側にあって

\[\angle{\mathrm{APB}}=\angle{\mathrm{AQB}}\]

ならば，4点 $\mathrm{A},\mathrm{B},\mathrm{P},\mathrm{Q}$ は1つの円周上にある．

円周角の定理の逆

次の図で， $\angle{x}$ の大きさを求めよ．

  1. $\angle{\text{ABD}}=\angle{\text{ACD}}=30^\circ$ より，

    2. 4点 $\text{A},\text{B},\text{C},\text{D}$ は同一円周上にある．

    $\angle{\text{CBD}}=\angle{\text{CAD}}=40^\circ$ より，

    $\triangle{\mathrm{BCD}}$ において，

    \[\angle{x}=180^\circ-(40^\circ+81^\circ+30^\circ)=\boldsymbol{29^\circ}\]
  2. $\angle{\text{CAD}}=180^\circ-(118^\circ+30^\circ)=32^\circ$

    3. $\angle{\text{CAD}}=\angle{\text{CBD}}$ より，

    4点 $\text{A},\text{B},\text{C},\text{D}$ は同一円周上にある．

    \[\angle{x}=\angle{\text{ACD}}=\boldsymbol{30^\circ}\]
  3. $\angle{\text{CAD}}=42^\circ-27^\circ=15^\circ$

    4. $\angle{\text{CAD}}=\angle{\text{CBD}}$ より，

    4点 $\text{A},\text{B},\text{C},\text{D}$ は同一円周上にある．

    \begin{align} \angle{x}&=\angle{\text{ABD}}\\ &=180^\circ-(98^\circ+27^\circ+15^\circ)\\ &=\boldsymbol{40^\circ} \end{align}

円に内接する四角形の定理

円に内接する四角形の定理

円に内接する四角形の定理

無題

無題

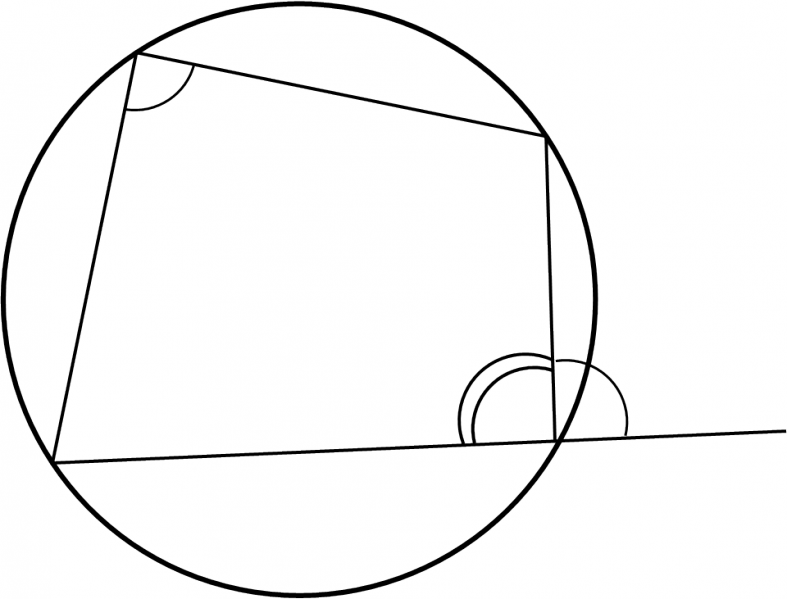
円に内接する四角形について，次の2つが成り立つ．

  1. 対角の和は $180^\circ$ である．
  2. 内角は，その対角の外角に等しい．

証明

円に内接する四角形の定理

次の図で， $\angle{x},\angle{y}$ の大きさを求めよ．

  1. \[\angle{x}=180^\circ-110^\circ=\boldsymbol{70^\circ},\angle{y}=\boldsymbol{120^\circ}\]
  2. $\angle{\text{BAD}}=180^\circ-100^\circ=80^\circ$ より，
    3. \[\angle{x}=180^\circ-(80^\circ+55^\circ)=\boldsymbol{45^\circ}\]
  3. \[\angle{x}=78^\circ\times2=\boldsymbol{156^\circ}\]
  4. $\angle{\text{CAD}}=86^\circ-52^\circ=34^\circ$ より，
    5. \[\angle{x}=180^\circ-34^\circ\times2=\boldsymbol{112^\circ}\]
  5. $\triangle{\text{ABC}}$ は $\text{AB}=\text{AC}$ の二等辺三角形だから，
    6. \[\angle{\text{ABC}}=(180^\circ-50^\circ)\times\frac{1}{2}=65^\circ\]， \[\angle{x}=180^\circ-65^\circ=\boldsymbol{115^\circ}\]
  6. $\triangle{\text{OCD}}$ は $\text{OC}=\text{OD}$ の二等辺三角形だから，
    7. \[\angle{\text{COD}}=180^\circ-38^\circ\times2=104^\circ,\] \[\angle{x}=104^\circ\times\frac{1}{2}=\boldsymbol{52^\circ}\]

    $\angle{\text{BCD}}=180^\circ-112^\circ=68^\circ$ より， $\triangle{\mathrm{BCD}}$ において，

    \[\angle{y}=180^\circ-(52^\circ+68^\circ+38^\circ)=\boldsymbol{22^\circ}\]