チェバの定理
チェバの定理
チェバの定理
チェバの定理
無題
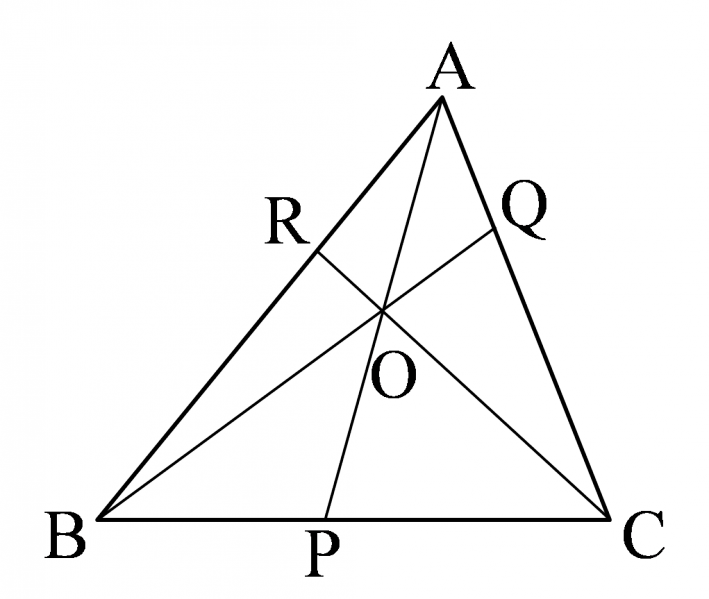
$\triangle{\mathrm{ABC}}$ の内部に点 $\mathrm{O}$ がある。頂点 $\mathrm{A},\mathrm{B},\mathrm{C}$ と $\mathrm{O}$ を結ぶ直線が向かい合う辺と,それぞれ $\mathrm{P},\mathrm{Q},\mathrm{R}$ で交わるとき
\[\frac{\mathrm{BP}}{\mathrm{PC}}\cdot\frac{\mathrm{CQ}}{\mathrm{QA}}\cdot\frac{\mathrm{AR}}{\mathrm{RB}}=1\]証明
チェバの定理
無題

$\angle{\text{A}}=90^\circ,\text{AB}=3,\text{AC}=4$ の $\triangle{\mathrm{ABC}}$ がある.点 $\text{A}$ から辺 $\text{BC}$ に垂線を引き交点を $\text{P}$ とする.また, $\angle{\text{B}}$ の二等分線と線分 $\text{AP}$ ,辺 $\text{CA}$ との交点をそれぞれ $\text{Q},\text{R}$ とし,直線 $\text{CQ}$ と辺 $\text{AB}$ との交点を $\text{S}$ とする.このとき, $AS:SB$ を求めよ.
$\text{BC}=\sqrt{3^2+4^2}=5$
また, $\triangle{\mathrm{ABC}}\backsim\triangle{\mathrm{PBA}}$ より, $\text{BP}=\dfrac{9}{5}$,
$\triangle{\mathrm{ABC}}\backsim\triangle{\mathrm{PAC}}$ より, $\text{PC}=\dfrac{16}{5}$
よって, $BP:PC=9:16$ となる.一方, $CR:RA=BC:BA=5:3$ である.
チェバの定理より,
\begin{align} \frac{\text{BP}}{\text{PC}}\cdot\frac{\text{CR}}{\text{RA}}\cdot\frac{\text{AS}}{\text{SB}}&=1\\ \frac{9}{16}\cdot\frac{5}{3}\cdot\frac{\text{AS}}{\text{SB}}&=1\\ \frac{\text{AS}}{\text{SB}}&=\frac{16}{15}\\ AS:SB&=\boldsymbol{16:15} \end{align}